Метод Сімпсона.
Цей метод більш точний у порівнянні з методами прямокутників та трапецій.
Формула Сімпсона (також Ньютона-Сімпсона) відноситься до прийомів чисельного інтегрування. Отримала назву на честь британського математика Томаса Сімпсона (1710-1761).
Суть прийому полягає у наближенні підінтегральної функції на відрізку [a, b] інтерполяційним многочленом другого ступеня p2(x), тобто наближення графіка функції на відрізку параболою.
Геометрично ілюстрація формули Сімпсона у тому, що у кожному з здвоєних часткових відрізків замінюємо дугу даної кривої дугою графіка квадратного тричлена.
За формулою Сімпсона при деякому етапі h обчислюють інтеграл. Потім крок збільшують удвічі та знову обчислюють інтеграл. Друге, грубіше обчислення інтеграла служить з метою оцінки точності першого, більш точного. Усі цифри першого та другого обчислень збігаються в результаті, а також перша неточна цифра більш точного результату вважаються вірними. Наприклад, якщо точніше обчислення число 1,4673, а друге - 1,4657, то 1,467 - правильне значення інтеграла (у ньому 4-значні цифри - вірні).
Для більш грубого розрахунку ніяких інших підготовчих робіт не потрібно. Значення xi та y(xi) беруться через одне. Слід лише врахувати, що з першому (точнішому) розрахунку необхідно вибрати таку кількість точок розбиття, яке кратно 4 тобто. ділиться на чотири. Якщо при вибраному вихідному кроці h необхідна точність результату не досягнута, то проводять третє, четверте обчислення з рівним кроком половині вихідного і т.д.
Розіб'ємо відрізок інтегрування [a; b] на 2× n рівних частин довжини. Позначимо точки розбиття x0 = a; x1=x0+h, ... , xi=x0+i× h, ..., x2n=b. Значення функції f у точках xi позначимо yi, тобто. yi = f (xi). Тоді згідно з методом Сімпсона:
Геометричний зміст формули Сімпсона: площа криволінійної трапеції під графіком функції f(x) на відрізку [a, b] приблизно замінюється сумою площ фігур, що лежать під параболами на малюнку 1.
Реалізація цього метода у середовищі Lazarus (інформатика, 8-9 класи):
Проект на Google Disk
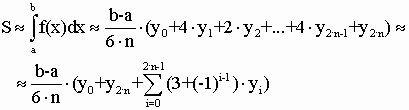




Немає коментарів:
Дописати коментар