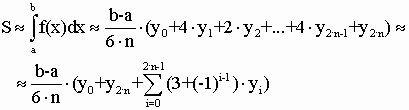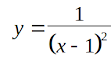субота, 21 червня 2025 р.
четвер, 19 червня 2025 р.
середа, 18 червня 2025 р.
вівторок, 17 червня 2025 р.
пʼятниця, 13 червня 2025 р.
четвер, 12 червня 2025 р.
середа, 11 червня 2025 р.
субота, 7 червня 2025 р.
четвер, 5 червня 2025 р.
понеділок, 2 червня 2025 р.
Використання інтерактивної дошки Intboard на уроках математики
На уроках математики я використовую програмне забезпечення для інтерактивної дошки Intboard Easy Start v. 2.0. Ця дошка має достатню кількість інструментів для роботи і дозволяє використовувати її учням.
Основні функції:
1. Кілька
режимів екрану: віконний режим, повноекранний режим, режим анотації.
2. Велика кількість навчальних матеріалів, предметних інструментів. Додані
математичні, фізичні та хімічні інструменти.
3. Користувач може створювати різні види графіків і гістограм.
4. Формули. Дозволяє користувачеві вставляти формули на сторінку.
5. Різні ефекти зміни сторінки.
6. Чарівне перо. При використанні чарівного пера, написи повільно зникають і
сторінка стає чистою; при кресленні кола викликається інструмент
підсвічування; при кресленні прямокутника викликається інструмент
збільшення.
7. Підтримка режиму мульти-тач. Дозволяє двом користувачам одночасно працювати
з інтерактивною дошкою.
8. Функція відображення фонової сітки. Дозволяє користувачеві відображати сітку
і редагувати її стиль.
9. Блокування екрану. Дозволяє користувачеві блокувати програму для захисту
даних.
10. Інструменти: запис, збільшення, годинник, клавіатура, калькулятор і т. д.
11. Зовнішні інструменти. Дозволяє користувачеві додавати додаткові інструменти
з комп'ютера в ПЗ дошки.
12. Переміщення панелі інструментів до верхнього або нижнього краю в
повноекранному режимі.
13. Малювання ліній під час використання математичних інструментів.
14. Функція вставки зовнішніх малюнків за допомогою гарячих клавіш (Ctri +
V).).
15. Функція програвання сторінки.
16. GOOGLE пошук. Дозволяє користувачам шукати ресурси і зображення за
допомогою Google, з подальшою вставкою на сторінку програми.
Можна колективно розв’язувати задачі і вправи. При роботі з дошкою
використовую графічний планшет. Результат роботи можна зберегти у форматі PDF і
розмістити у Google Classroom. (приклад, червоним олівцем користується
учитель, іншими кольорами – учні. Файл імпортовано у формат PDF).
субота, 31 травня 2025 р.
понеділок, 26 травня 2025 р.
субота, 17 травня 2025 р.
вівторок, 29 квітня 2025 р.
субота, 12 квітня 2025 р.
Похідна у завданнях ЗНО і НМТ
 | ||
НМТ, 14.06.2024
|
 |
| НМТ, 08.06.2023, 2 зміна |
 |
| НМТ, 13.06.2023, 1 зміна |
 |
| НМТ, 14.06.2023, 2 зміна |
 |
| Завдання ЗНО |
 |
| Завдання ЗНО |
Обчислення інтегралів у Microsoft Mathematics
 |
Ввести формулу функції. Обрати кнпку обчислення похідної. |
Похідна у GeoGebra
Відкрити GeoGebra Класична. Ввести формулу функції.
 |
| Натиснути кнопку обчислення похідної. Обрати графік похідної. |
Обчислення похідної у Advanced Grapher
Advanced Grapher - робота з графіками і функціями. Це досить потужна, але легка у використанні програма. Призначена для побудови графіків, креслення кривих і обчислення функцій. За допомогою цієї програми можна обчислити похідну функції та побудувати графік похідної.
Приклад.
 |
| Вводимо формулу функції. |
 |
| Графіки функції та її похідної (зеленого кольору). |
Найбільше і найменше значення функції на проміжку
1. Якщо функція неперервна на відрізку, тоді вона досягає на ньому і свого найбільшого, і свого найменшого значень (ця теорема доводиться в курсі вищої математики).
2. Найбільшого і найменшого значень безперервна функція може досягати як на кінцях відрізка, так і всередині нього.
3. Якщо найбільше (або найменше) значення досягається всередині відрізка, тоді тільки в стаціонарній або критичній точці.
Алгоритм знаходження найменшого та найбільшого значень неперервної функції на відрізку :
1. Знайти похідну f'(x).
2. Знайти стаціонарні та критичні точки функції, що лежать всередині відрізка [a;b]
3. Обчислити значення функції y=f(x)
ymax) і найбільше (це буде ymin
Приклад 1.
пʼятниця, 28 лютого 2025 р.
четвер, 20 лютого 2025 р.
Обчислення інтегралів у Lazarus
Метод Сімпсона.
Цей метод більш точний у порівнянні з методами прямокутників та трапецій.
Формула Сімпсона (також Ньютона-Сімпсона) відноситься до прийомів чисельного інтегрування. Отримала назву на честь британського математика Томаса Сімпсона (1710-1761).
Суть прийому полягає у наближенні підінтегральної функції на відрізку [a, b] інтерполяційним многочленом другого ступеня p2(x), тобто наближення графіка функції на відрізку параболою.
Геометрично ілюстрація формули Сімпсона у тому, що у кожному з здвоєних часткових відрізків замінюємо дугу даної кривої дугою графіка квадратного тричлена.
За формулою Сімпсона при деякому етапі h обчислюють інтеграл. Потім крок збільшують удвічі та знову обчислюють інтеграл. Друге, грубіше обчислення інтеграла служить з метою оцінки точності першого, більш точного. Усі цифри першого та другого обчислень збігаються в результаті, а також перша неточна цифра більш точного результату вважаються вірними. Наприклад, якщо точніше обчислення число 1,4673, а друге - 1,4657, то 1,467 - правильне значення інтеграла (у ньому 4-значні цифри - вірні).
Для більш грубого розрахунку ніяких інших підготовчих робіт не потрібно. Значення xi та y(xi) беруться через одне. Слід лише врахувати, що з першому (точнішому) розрахунку необхідно вибрати таку кількість точок розбиття, яке кратно 4 тобто. ділиться на чотири. Якщо при вибраному вихідному кроці h необхідна точність результату не досягнута, то проводять третє, четверте обчислення з рівним кроком половині вихідного і т.д.
Розіб'ємо відрізок інтегрування [a; b] на 2× n рівних частин довжини. Позначимо точки розбиття x0 = a; x1=x0+h, ... , xi=x0+i× h, ..., x2n=b. Значення функції f у точках xi позначимо yi, тобто. yi = f (xi). Тоді згідно з методом Сімпсона:
Геометричний зміст формули Сімпсона: площа криволінійної трапеції під графіком функції f(x) на відрізку [a, b] приблизно замінюється сумою площ фігур, що лежать під параболами на малюнку 1.
Реалізація цього метода у середовищі Lazarus (інформатика, 8-9 класи):
Проект на Google Disk
середа, 19 лютого 2025 р.
Обчислення визначених інтегралів у системі Maple
Робота в Maple проходить в режимі сесії – користувач вводить команди, вирази або процедури, які сприймаються і обробляються Maple. В кінці кожної команди ставиться або крапка з комою «;» (під відповідним виразом буде виведено результат виконання команди або повідомлення про помилку), або двокрапка «:» (результат не виводиться). Робоче поле поділяється на три частини:
1) область введення – складається з командних рядків. Кожен командний рядок починається з символа «>»;
2) область виведення – містить результати обробки введених команд в вигляді аналітичних виразів, графічних об’єктів або повідомлень про помилку;
3) область текстових коментарів – містить довільну текстову інформацію, яка може пояснити процедури, що обробляються.
Текстові рядки не сприймаються Maple та не обробляються.
Приклад обчислення інтегралів:
Обчислення інтегралів у Microsoft Mathematics
Microsoft Mathematics
Математичні інструменти Microsoft Mathematics:
- Графічний калькулятор — модуль, для побудови 2-D та 3-D графіків в різних системах координат (декартова, полярна, сферична, циліндрична).
- Обчислювач рівнянь — модуль, створений для вирішення одного рівняння або системи рівнянь.
- Бібліотека формул та рівнянь — модуль для пошуку часто вживаних формул з математики та інших галузей науки, їх графічного дослідження, обчислення для конкретної змінної.
- Обчислювач трикутника — модуль для знаходження невідомих сторін та кутів трикутника по відомим.
- Конвертер величин — модуль для перетворення вимірювань з однієї системи одиниць в іншу (довжини, площі, обсягу, ваги, температури, тиску, енергії, сили, швидкості, часу).\
Приклад обчислення інтеграла:
Обчислення визначених інтегралів в GeoGebra
У програмi GeoGebra всi iнтеграли розв’язуються однаково. Програма має простi команди для знаходження як визначених iнтегралiв, так i невизначених iнтегралiв.
Приклад обчислення інтеграла:
Обчислення визначених інтегралів у Advanced Grapher
Комп'ютерна програма Advanced Grapher
Унікальна програма для застосування при вивченні шкільного курсу математики. Дозволяє на одній координатній площині зображувати:
- графіки функцій f(x), f(x+a), f(x-a) a>0
- графіки функцій f(x), f(x)+b, f(x)-b>0
- графіки функцій f(kx+b)+c, |f(kx+b)+c|, f(|kx+b|)+c
- графік y=f(x,, одночасно визначити похідну і побудувати графік похідної;
- рішення систем рівнянь і нерівностей основного і поглибленого рівнів.
Комп'ютерна програма дозволить учням вирішувати дослідницькі завдання: на визначення увігнутості, опуклості кривих, у побудові дотичної і нормалі в будь-якій точки області визначення функції, дослідження точок максимуму і мінімуму, найбільшого і найменшого значень на проміжку, визначення площі фігури, обмеженої лініями.
Продемонструємо, як виконується побудова криволінійних трапецій та обчислення їх площ у
програмі Advanced Grapher на прикладах.
Приклад 1. Знайдіть площу криволінійної трапеції, обмеженої графіком функції
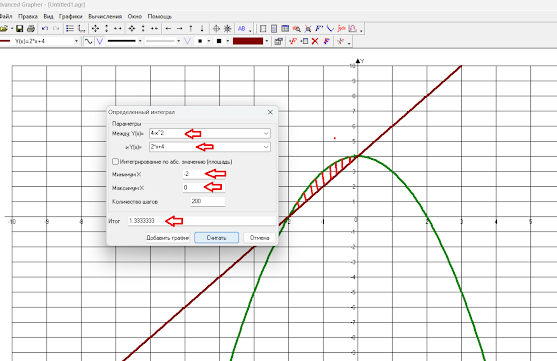
і прямими y 0,= x = -1, x =0.Advanced Grapher Version 2.2), натискаємо кнопку «Добавить график» на панелі
інструментів – на рис.1 ця кнопка підсвічена.
панелі інструментів (рис. 1) кнопку
Після чого внесемо у вікно, що відкрилось, дані (рис. 4) і натиснемо кнопку «Считать». У рядку «Итог» побачимо чисельний результат для площі заданої трапеції. Натиснувши кнопку «Добавить график» (рис. 4), виберемо варіант штриховки трапеції і на екрані побачимо саму трапецію (рис. 5). Щоб збільшити або зменшити масштаб графіків по осях, є кнопки на панелі інструментів (на рис.5 масштаб збільшений по осях Ох та Оу).
Приклади обчислення інтеграла і площі плоскої фігури:
